TimesNet

引言

TimesNet是Tsinghua发表在ICLR 2023上的一篇论文，将时间序列按周期内变化和周期间变化两个视角建模，在时序预测，补全，分类，异常检测上达到了SOTA的性能。

TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis

时间序列数据分析在天气预报，金融预测，工业监控等领域有着广泛的应用。与语言或视频数据不同，一般单个数据点的时序数据无法提供足够的信息，目前的研究大多集中在时间的变化特征，如连续性，周期性，趋势性等。

使用深度学习方法进行时间序列分析的研究包括以下几种：

• 基于Markov假设，使用RNN等对连续时间点进行建模，这种方法难以捕捉长期依赖，并且计算效率低
• 使用CNN在时间维度上进行卷积操作，但是一维卷积核具有局部性特征，无法捕捉长期依赖关系
• 基于transformer的模型使用注意力机制捕捉时间点之间的成对依赖关系，但是关注于分散的时间点，无法捕捉时间序列的整体变化特征

时序数据通常呈现多周期性特征，如天气观测中的日际与年际变化，TimesNet考察这种周期内与周期间的变化，周期内变化(intraperiod-variation)指一个周期内的短期变化模式，周期间变化(interperiod-variation)则是指连续不同周期的长期趋势。TimesNet将一维时间序列重构为二维张量，每列对应周期内的时间点，每行则对应不同周期内的同一相位的时间点，最终构建时间维度的二位波动特征。

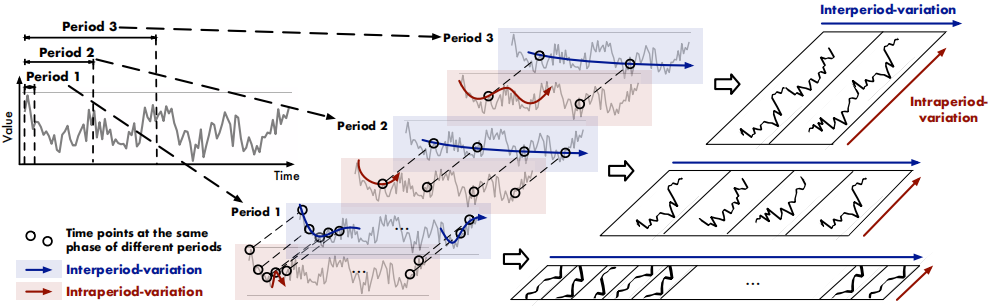
上图展示了3个不同的周期长度设置的周期内变化和周期间变化，红色线显示了一个周期内的短期模式变化，蓝色线显示连续多个周期间的趋势性变化。

TimesNet模型

Transform 1d-variations into 2d-variations

在TimesNet中，每个时间点受两类变化影响，一种是相邻区域变化，另一种是不同周期相同相位上的变化，即周期内变化和周期间变化。TimesNet首先考虑将一维时间序列转换为二维结构化信息。

包含个record variates的长度为T的时间序列，其1维形式可表示为

为建模周期间的变化，首先发现序列中的周期长度，TimesNet使用了快速傅里叶变换(Fast Fourier Transform, FFT)在频域分析上述序列。

傅里叶变换的思想是指，任何时域上的信号都可以表示为一组正弦波的叠加，这些正弦波有不同的频率，振幅和相位，换言之，傅里叶变换是将时域信号转换为频域信号。

频域是指用频率成分来描述信号的方式，时域是指用时间变化来描述信号

快速傅里叶变换是一种快速计算离散傅里叶变换的算法，能够高效地将时域信号转换为频域信号。
其计算公式为

其中是频域信号的第个频率分量，是时域信号的第个采样值，是信号长度。

FFT Example

即使用FFT分析序列$\mathbf{X}{1D}k{f_1,\cdots,f_k}{\mathbf{A}{f_1},\cdots,\mathbf{A}_{f_k}}\lceil \frac{T}{f_i}\rceil, i\in{1,\cdots,k}{p_1,\cdots,p_k}$

上述的操作记为，即

则将原序列填充至长度为后可得到个二维矩阵，即

$$
\mathbf{X}^i_{2D} = \text{Reshape}{p_i,f_i}(\text{Padding}(\mathbf{X}{1D})), i\in {1,\cdots,k}
$$

程序实现示例如下，假设序列长度为，

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq

# 设置采样参数
Fs = 500  # 采样频率（Hz）
T = 1.0 / Fs  # 采样周期
L = 1000  # 采样点数,序列长度
x = np.linspace(0.0, L*T, L, endpoint=False)  # 时间序列

# 构造信号：混合两个正弦波，分别为55Hz,95Hz
f1, f2 = 55, 95
signal = 0.2 * np.sin(2.0*np.pi*f1*x) + 0.5 * np.sin(2.0*np.pi*f2*x)

# 添加少量噪声
np.random.seed(0)
signal += 0.1 * np.random.normal(size=L)

print(f"{signal.shape = }")


# 计算FFT
yf = fft(signal) # 计算傅里叶变换，输出复数列表，a+bi，复数的模为振幅，tan^-1(b/a)为相位
xf = fftfreq(L, T)[:L//2]  # 得到yf中每个正弦波的频率，实数信号的FFT是共轭对称的，负频率部分是冗余的，只取正数频率部分

print(f"{yf.shape = }, {yf[0] = }")
print(f"{xf.shape = }, {xf[0] = }")

top_k = 2 # 超参数设置

A = np.abs(yf[:L//2]) # 各正弦波的振幅

idx = np.argsort(A)[-top_k:] # 取前top_k个振幅最大的频率
print(f"{A[idx] = }")

for i in range(top_k):
    fi = xf[idx[i]] # 频率
    pi = np.ceil(L/fi) # 向上取整，周期数量
    print(f"{fi = }, {pi = }")

    pad_width = int(np.ceil(fi*pi)) - L
    Xi = np.pad(signal,pad_width=(0, pad_width), mode='constant',constant_values=0)
    print(f"{Xi.shape = }")

    Xi_2D = np.reshape(Xi,(int(pi),int(fi)))
    print(f"{Xi_2D.shape = }")

输出如下：

signal.shape = (1000,)
yf.shape = (1000,), yf[0] = np.complex128(-4.525670749019317-0j)
xf.shape = (500,), xf[0] = np.float64(0.0)
A[idx] = array([ 97.56053856, 251.0764452 ])
fi = np.float64(55.0), pi = np.float64(19.0)
Xi.shape = (1045,)
Xi_2D.shape = (19, 55)
fi = np.float64(95.0), pi = np.float64(11.0)
Xi.shape = (1045,)
Xi_2D.shape = (11, 95)

TimesBlock

整个TimesNet的网络架构由多个TimesBlock通过残差堆叠而成，首先将原始输入$\mathbf{X}{1D}\mathbf{X}{1D}^{0}\in\mathbb{R}^{T\times d_{model}}$，其余各层由残差连接，用下式表示

$$
\mathbf{X}{1D}^{l} = \mathbf{X}{1D}^{l-1} + \text{TimesBlock}(\mathbf{X}_{1D}^{l-1})
$$

网络结构如下图所示：

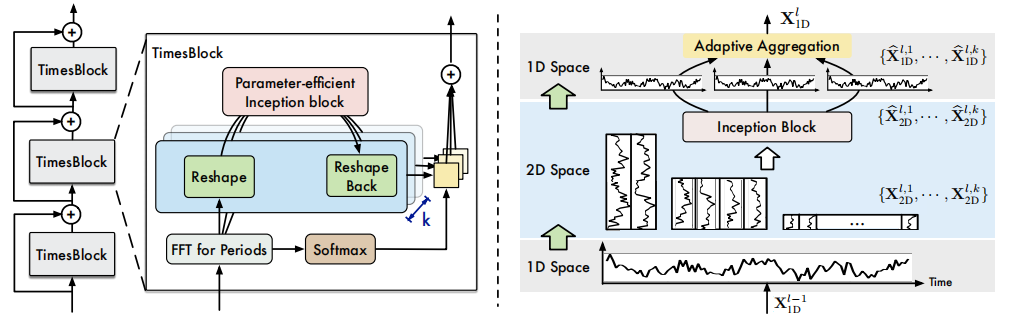
TimsBlock会将$\mathbf{X}{1D}^{l-1}\mathbf{X}{2D}^{l-1}p$为周期数，执行Inception操作，该操作可使用多种网络结构，如ResNet,ConvNet等。每个Block的计算过程如下

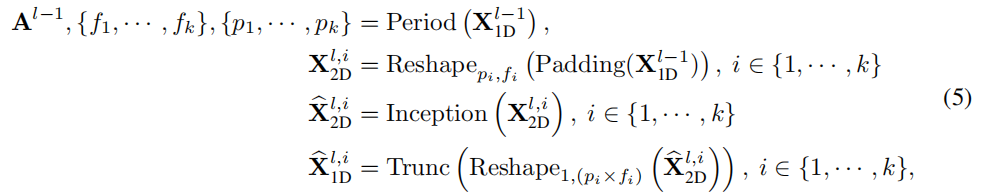
得到每个频率对应的一维时间序列$\mathbf{\hat{X}}{1D}^{i,l}\mathbf{X}{1D}^{l}$

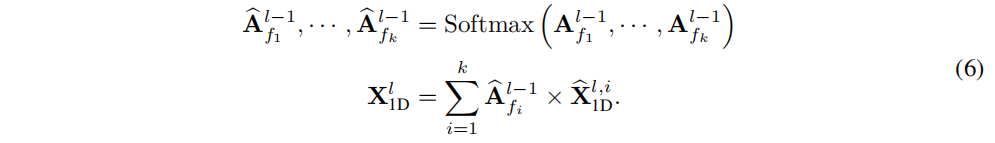
Experiments

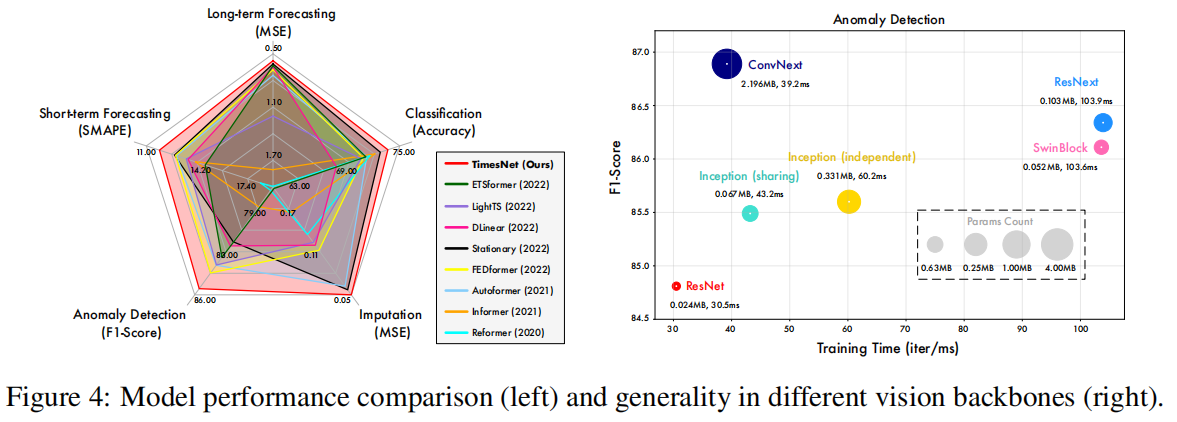
TimesNet在多个数据集上进行了实验，包括时序预测，分类，缺失值填补，异常检测等任务。结果表明，TimesNet在这些任务上均达到了SOTA的性能。下图展示了TimesNet在各种任务上与baseline模型的比较。

的设置

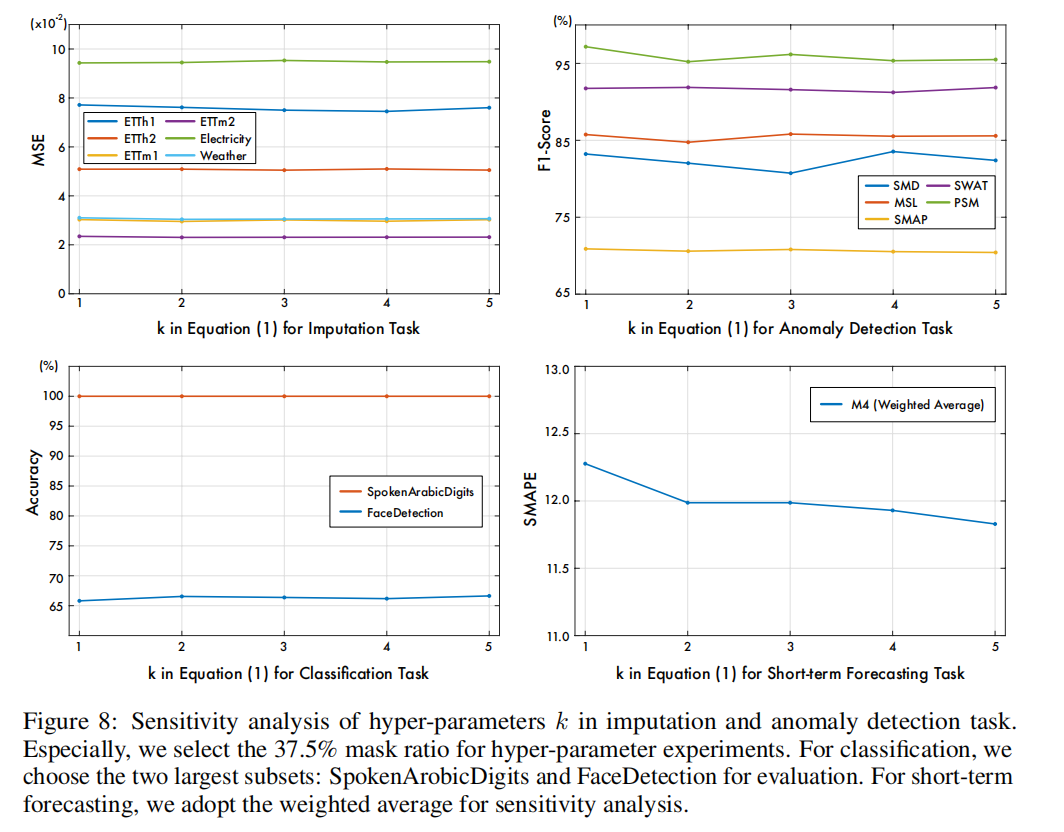
在TimesNet中，根据输入的值计算

在TimesNet中，作者根据不同的数据集特点设置了不同的和。

的设置

作者针对4项任务对不同的值进行了实验，结果表明，的设置对模型性能影响不大。

Conclusion

TimesNet通过将一维时间序列转换为二维结构化信息，能够更好地捕捉时间序列的周期内变化和周期间变化特征。通过多层TimesBlock的堆叠，TimesNet在多个时序分析任务上达到了SOTA的性能。将Inception操作与更强的backbone网络结合，有望进一步提升模型性能。